When building a predictive model it is a good idea to do a univariate analysis, before throwing the whole bunch in a complex algorithm. This way we get a feel for the potential contribution of each predictor. When a lot of predictors are available one can often make a first selection and only use predictors that show univariate predictive power. Not having to sift through loads of unpromising variables can speed up learning algorithms significantly. Besides, knowing the individual predictive value can improve the data scientist’s discussion with business people. Especially when it is combined with a correlation analysis of the predictors. Due to multicollinearity variables with known predictive value might not end up in the model, which can lead to distrust towards the data scientist’s work. It is essential to report properly why some variables did not make it to a final model.
Searching for a measure
I have been searching for a good one-size-fits-all measure for expressing the individual predictive value for quite some time now. Since most of the predictive models are classification problems, I mainly focused on this type of measures. I have experimented with fitting a univariate logistic regression model on the predictor and measure the deviance reduction. This, however, does not work well if; the relationship is nonlinear, the predictor is zero-inflated, or the predictor contains many missing values. Of course, when adding appropriate dummies or polynomials these problems could be overcome, but non-automated ways of calculating the predictive values can get very tedious.
The gini
In the financial industry, where I am currently employed, the gini is the standard of expressing both univariate and multivariate predictive value. The latter after modeling of course. For an individual predictor the gini is calculated in the following way:
- sort both the predictor and the target by the predictor, low to high.
- for each unique value of the predictor:
- “predict” the target by giving all smaller values the label 0 and the equal and larger values the label 1.
- calculate the contingency table: TN, TP, FN, FP
- calculate the Sensitivity = TP / TP + FN and the Specificity = TN / TN + FP
- determine ROC curve; x-axis = 1 - Specificity (False Negative Rate), y-axis = Sensitivity (False Positive Rate).
- take the AUC of the ROC curve, subtract 0.5, multiply by 2.
Doing some research into this measure, I did not find it satisfactory either for univariate purposes. The first obvious drawback is that the gini cannot be calculated for categorical predictors. We always need a second measure when also dealing with categoricals. Moreover, although being able to handle nonlinearity, it still fails when the variable is zero-inflated. Take the following example plot, with the predictor on the x-axis, the target on color and the y-axis displaying meaningless jitter so the points do not overlay each other. (For the code of the functions used, see the bottom of the post).
library(tidyverse)
set.seed(9999)
x <- runif(1000, 0, 20)
x_with_error <- x + rnorm(1000, 0, 3)
y <- as.numeric(x_with_error < 5)
x_zero_inflated <- x
x_zero_inflated[sample(1:1000, 700)] <- 0
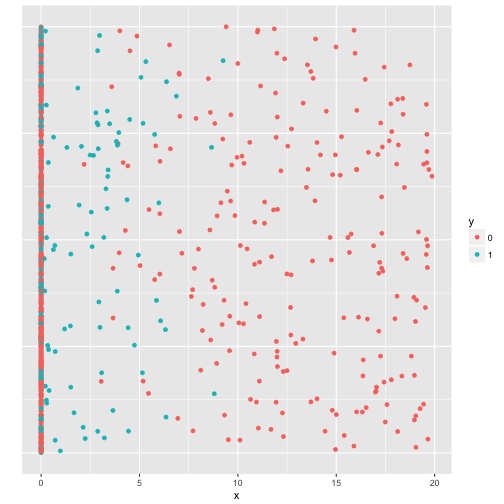
predictor_plot(x_zero_inflated, y)
gggini(x_zero_inflated, y)
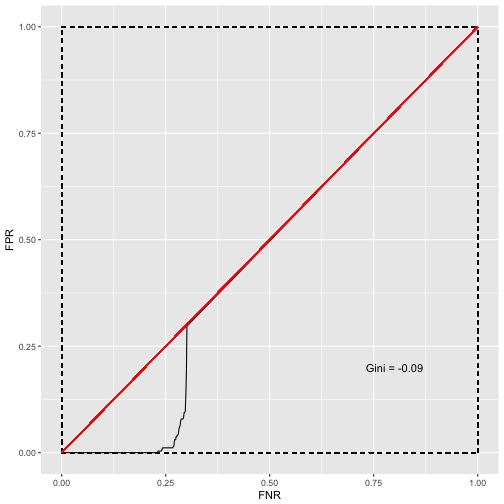
In the above situation the predictor has a lot of predictive value for non-zero cases. Since the zeros are assigned randomly and there are more non-cases than cases, the non-cases dominate the zero region. The low, non-zero region of the predictor has more cases, and the high region has more non-cases. This results even in a negative gini, where the measure should be between 0 and 1. That the gini cannot deal with local regions, even when the predictor is not value-inflated and there are as many cases as non-cases, is shown in the following example.
y2 <- as.numeric(x_with_error > 5 & x_with_error < 15)
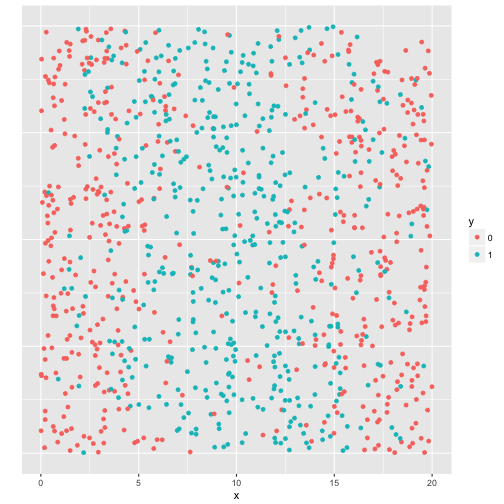
predictor_plot(x, y2)
gggini(x, y2)
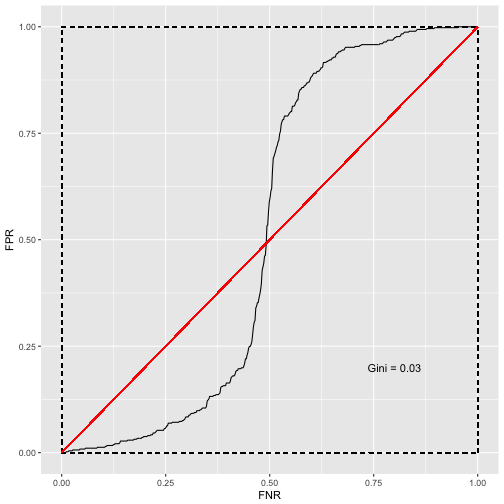
We get a sigmoid ROC curve, because all the cases are situated in the middle of the predictor. Clearly, also the gini has too many shortcomings to serve as one-size-fits-all univariate testing method.
The tree-based Kappa
Okay, so if it is not the gini either, what should we use? What can capture categorical and numerical predictors, does allow for zero-inflatedness (is that a word?, mmm, I’ll go with it anyway), is able to deal with local regions and can even handle missing values? The classification tree! Maybe not the best model for complex multivariate situation, due to its tendency to overfit, but perfect here. Here is a simple way to express the univariate predictive power:
- use k-fold cross validation; train a univariate tree and obtain hold-out probabilities.
- find the optimal split of the predictions, or just split on 0.5.
- calculate Cohen’s Kappa on these predictions and the actual y-values.
For the tree fitting I use the rpart package with its default settings, but you can of course play around with the tree parameters. Calculating the Kappas on the above situations gives results that we would expect, given the amount of predictive value:
# the ordinary situation, that gini would do well on too.
get_kappa(x, y)
## [1] 0.679
# the zero-inflated predictor.
get_kappa(x_zero_inflated, y)
## [1] 0.305
# the cases in the middle of the predictor.
get_kappa(x, y2)
## [1] 0.469
In all situations the kappa indicates that the predictions made with the cross-validated classifications trees, are a lot better than we might expect from chance.
I am quite excited about this way of expressing univariate predictive value, I have not discovered a situation yet that this method cannot deal with. If you think there are any flaws in my thinking, or you can think of even a better method, please leave a comment!
As promised, here you find the full set of functions that were used for this writing. As always, the functions can be imported from the github package accompanying this blog. Just run devtools::install_github("edwinth/thatssorandom").
library(tidyverse)
predictor_plot <- function(x, y) {
stopifnot(x %>% is.numeric)
stopifnot(y %>% unique %>% length %>% `==`(2))
data_frame(x = x, y = as.factor(y), y_axis = 0) %>%
ggplot(aes(x, y_axis)) +
geom_jitter(aes(col = y)) +
ylab('') +
theme(axis.text.y = element_blank(),
axis.ticks.y = element_blank())
}
gggini <- function(x, y) {
roc_obj <- pROC::roc(y, x)
roc_plot <- data_frame(FPR = roc_obj$sensitivities,
FNR = 1 - roc_obj$specificities) %>%
group_by(FNR) %>% summarise(FPR = max(FPR)) %>%
rbind(data_frame(FPR = 0, FNR = 0))
gini <- round(2 * (roc_obj$auc - 0.5), 2)
ggplot(roc_plot, aes(FNR, FPR)) +
geom_line() +
geom_segment(aes(0, 0, xend = 0, yend = 1), col = "black", lty = 2) +
geom_segment(aes(0, 1, xend = 1, yend = 1), col = "black", lty = 2) +
geom_segment(aes(0, 0, xend = 1, yend = 0), col = "black", lty = 2) +
geom_segment(aes(1, 0, xend = 1, yend = 1), col = "black", lty = 2) +
geom_segment(aes(0, 0, xend = 1, yend = 1), col = "red") +
annotate("text", x = 0.8, y = 0.2, label = sprintf("Gini = %s", gini))
}
# main function to obtain kappa, all others are helpers
get_kappa <- function(x, y, k = 10) {
stopifnot(length(unique(y)) == 2)
stopifnot(length(y) == length(x))
model_set <- data_frame(y = y,
x = x,
cv_grp = add_crosval_groups(length(y), k))
scored_set <- lapply(1:k, train_one_split, model_set = model_set) %>%
do.call("rbind", .) %>% as_data_frame
best_split <- determine_split(scored_set$`1`, scored_set$y)
y_hat_cat <- as.numeric(scored_set$`1` > best_split)
kappa <- calc_kappa(y_hat_cat, scored_set$y)
return(round(kappa, 3))
}
add_crosval_groups <- function(n, k) {
groups <- rep(1:k, n %/% k)
if ((n %% k) != 0) groups <- groups %>% c(1:(n %% k))
sample(groups)
}
train_one_split <- function(model_set, k) {
train <- model_set %>% filter(cv_grp != k)
hold_out <- model_set %>% filter(cv_grp == k)
mod <- rpart::rpart(y ~ x, data = train, method = "class")
yhat <- rpart::predict.rpart(mod, hold_out)
cbind(y = hold_out$y, yhat)
}
calc_kappa <- function(predicted, observed) {
ct <- table(observed, predicted)
if (!isTRUE(all.equal(dim(ct), c(2, 2)))) {
return(NA)
}
n <- sum(ct)
p_0 <- sum(diag(ct)) / n
m_y <- sum(ct[,1]) * sum(ct[1,]) / n
m_yhat <- sum(ct[,2]) * sum(ct[2,]) / n
p_e <- (m_y + m_yhat) / n
(p_0 - p_e) / (1 - p_e)
}
determine_split <- function(y_hat_num,
y,
splits = seq(0.01, 0.99, by = .01)){
y_hat_list <- map(splits, function(s) as.numeric (y_hat_num > s))
kappas <- map_dbl(y_hat_list, calc_kappa, observed = y)
max_splits <- which(kappas == max(kappas, na.rm = TRUE))
return_split <- max_splits[ ceiling(length(max_splits) / 2) ]
return(splits[return_split])
}
